Playing 2048 with Deep Q-Learning

Overview

Reinforcement learning is a machine learning method where the model learns to maximise the reward received through interacting with the environment. This particular field of machine learning has been exciting in recent years, followed by the huge success of AlphaGo developed by Deepmind. In this article, we will discuss a reinforcement learning algorithm, Deep Q-Learning, and see how this algorithm could learn to play the game of 2048 as well as how to implement it in Pytorch, a popular deep learning library.

The source code can be found in github:

https://github.com/qwert12500/2048_rl

Table of Contents

1. Game of 2048
2. Baseline result
3. What is reinforcment learning?
4. Improving the result with Deep Q-Learning

Game of 2048

Baseline Result

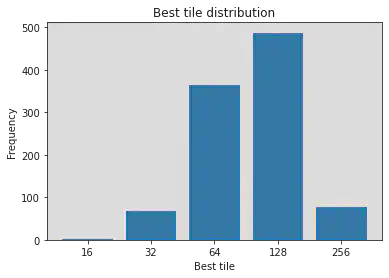
In this section, we will develop a naive strategy by selecting a random action until the game ends. There are 4 different possible actions in the game: Up, down, left or right. Obviously, this strategy is not optimal: Deciding the next action does not depend on the current state of the board. In later sections, we will develop deep Q-Learning which would make an intelligent decision by considering the current state and possible future rewards.

For the baseline experiment, 1000 simulations will be rolled out and see how each game performs and the scores that each game could get.

def sample_game_random():
    game = Board()
    finish = False
    while not finish:
        direction = np.random.randint(4)
        moved = main_loop(game, direction)
    if not moved:
        # Sample another direction if the move is invalid
        continue
    finish = game.is_game_over()
    total_score = game.total_score
    best_tile = game.board.max()
    return total_score, best_tilescores_random, best_tiles_random = [], []

for i in range(1000):
    total_score, best_tile = sample_game_random()
    scores_random.append(total_score)
    best_tiles_random.append(best_tile)

And the histogram of 1000 games sampled by taking random actions: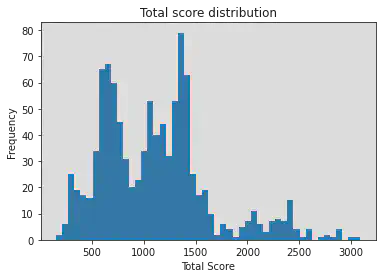

What is reinforcement learning?

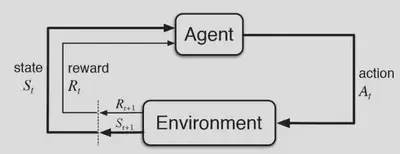
The above figure summarises the architecture of reinforcement learning: The agent interacts with the environment by performing actions, and then the state of the environment changes according to the choice of action with a corresponding reward. The agent then collects data (state, reward and action) and learns to take future actions that maximise the future reward.

A gentle introduction to reinforcement learning can be found in the following article: Reinforcement Learning 101.

But how can the agent learn to make the optimal action? This is where the reinforcement learning algorithm comes in. In particular, Q-Learning algorithm is considered. Q-Learning is a model-free approach with the following update equation in each training iteration: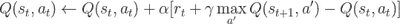

With Q(s,a) being the expected value of the current state s and taking action a. For small size of state-action pairs (s,a) we could update and compute the Q-value iteratively using the formula above under policy π until Q-value converges.

Improving the result with deep Q-Learning

To develop a model using deep Q-Learning, we have to first formalise the components required in reinforcement learning:

1. Environment: The board and the tiles
2. State: The configuration of the tiles on the board. Since the values of the tiles are discrete and are powers of 2, one-hot encoding is used for each tile.
3. Reward: The reward of each action is the score of each merging, i.e. the value of the new tile after the merge.
4. Value: The corresponding Q-value Q(s,a) associated with the state-action pair, as formulated in the previous section.
5. Policy: ε-greedy policy is used. For a probability ε the policy would choose random next action, and with probability 1-ε the policy would choose the action that yields the highest Q-value, i.e. action a that has the highest Q(s,a).

Although Q-Learning formula defined in the previous section provides a method to train the model, it is impractical in the game of 2048.

The number of states in the game is 16¹⁶, which is approximately 10¹⁹, since there are 16 spaces on the board, and each space can take 16 different values (0 (empty cell), 2, 4, …, 2¹⁵=32768). Therefore it is impossible to build a explicit mapping from state-action pair (s,a) to the corresponding Q-value. Instead, we have to consider using neural network as an approximation to the function Q(s,a) (therefore this approach is also known as deep Q-Learning).

The algorithm for Deep Q-Learning is outlined as follows:

• Size of memory buffer: 50000
• Optimizer: Adam
• Learning Rate: 5e-5
• γ: 0.99
• ε: Starting from 0.9 and decays by a factor of 0.9999 for each episode until it reaches 0.01 Batch size: 64

The architecture of the neural network composes of three convolutional blocks, within each block there are different convolutions of different kernel sizes, followed by 2 fully-connected layers, and each layer has Relu activation function.

class ConvBlock(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(ConvBlock, self).__init__()
        d = output_dim // 4
        self.conv1 = nn.Conv2d(input_dim, d, 1, padding='same')
        self.conv2 = nn.Conv2d(input_dim, d, 2, padding='same')
        self.conv3 = nn.Conv2d(input_dim, d, 3, padding='same')
        self.conv4 = nn.Conv2d(input_dim, d, 4, padding='same')

    def forward(self, x):
        x = x.to(device)
        output1 = self.conv1(x)
        output2 = self.conv2(x)
        output3 = self.conv3(x)
        output4 = self.conv4(x)
        return torch.cat((output1, output2, output3, output4), dim=1)

class DQN(nn.Module):

    def __init__(self):
        super(DQN, self).__init__()
        self.conv1 = ConvBlock(16, 2048)
        self.conv2 = ConvBlock(2048, 2048)
        self.conv3 = ConvBlock(2048, 2048)
        self.dense1 = nn.Linear(2048 * 16, 1024)
        self.dense2 = nn.Linear(1024, 4)

    def forward(self, x):
        x = x.to(device)
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        x = nn.Flatten()(x)
        x = F.dropout(self.dense1(x))
        return self.dense2(x)

Finally after training the model for 20000 episodes, some of the episodes does manage to reach tile 2048, for example the one below:

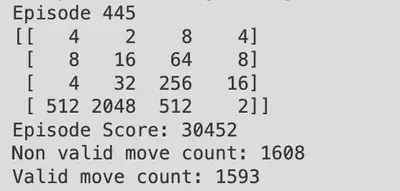
Although most of the time the agent could not reach 2048, due to the randomness induced (random new tiles) after each action, and neural network approximations are almost never perfect.

At last the agent plays 2048 with the trained network for 1000 episodes, in order to compare the improvement against baseline results:

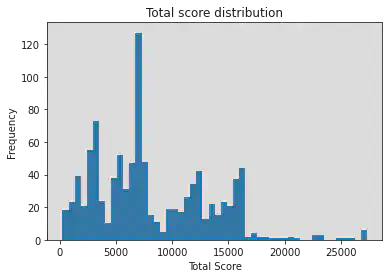
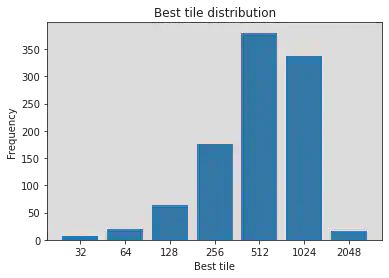
It seems that around 50% the agent could get tiles 1024 or above in the board when the game ends, which is much better than the baseline result!